The Merit Function

BOG optimizes a gem by maximizing a Merit Function. The Merit Function (or MF) is a numerical value assigned to the quality of a gemstone design, based on a set of user-specified criteria. BOG currently supports five different measures (or "Targets") of gem merit:

Gem ISO brightness (called ISO below) Quick Jump to ISO
Illumination response (called Ill below) Quick Jump to Ill
Tilt performance (called Tilt below) Quick Jump to Tilt
Sparkle or "action" (called Sparkle below) Quick Jump to Sparkle
Fire or dispersion (called Fire below) Quick Jump to Fire

The overall merit function is the mathematical sum of the merit functions of the individual targets, each multiplied by a weighting factor:

MF = (ISO_MF * ISO_Weight) + (Ill_MF * Ill_Weight) + (Tilt_MF * Tilt_Weight) + ...

BOG varies the pavillion and crown angles and evaluates the corresponding MF. Using a peak-finding algorithm (described here), the program zeroes in on the combination of angles which produces the highest Merit Function.

Merit Function Balance

You set the balance between the various targets using the General panel of the Specify Optimization Targets window. This window appears when you click on the Modify Targets button in BOG's main window.

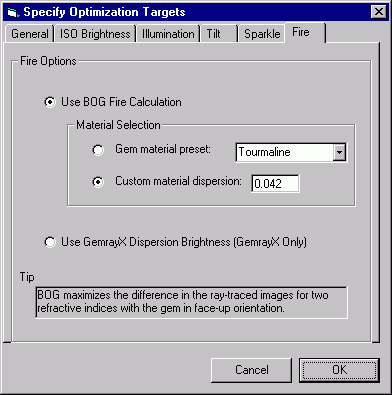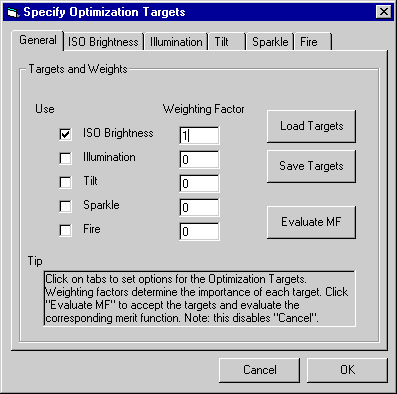
Targets and Weights

The Merit Function panel controls the balance between the various targets set in the other panels. Along the left side are a number of check boxes which allow you to Use (include or exclude) the various targets. Enter values in the Weighting Factor boxes to achieve the desired balance. Note: entering a weighting factor is not enough to include a particular target. You must also click the relevant Use box! This allows you to turn a target on and off while retaining the weighting factor.

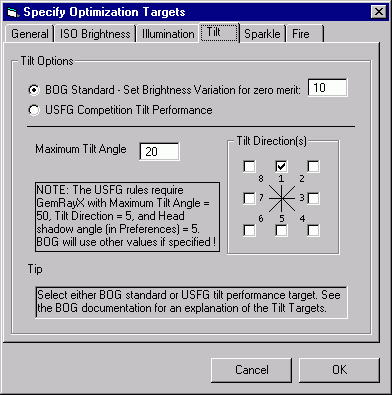
The other panels include numerous options to specify the conditions under which the various targets are evaluated. The Load Targets and Save Targets buttons allow you to manage your preferences using named text files. Feel free to examine the contents of these files using a text editor, but you probably shouldn't alter them outside of BOG

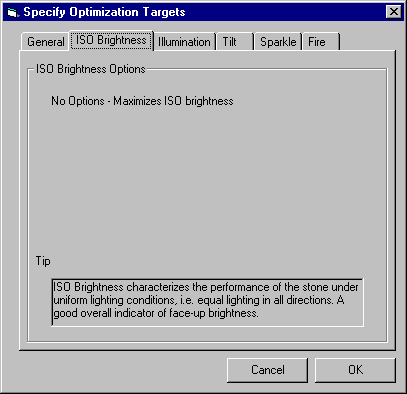
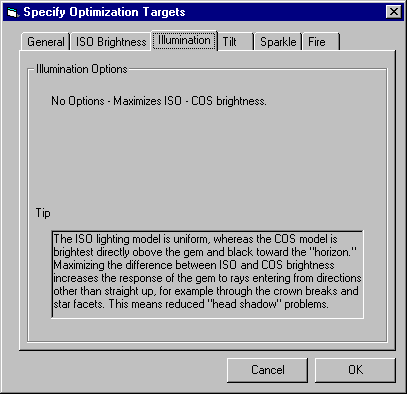
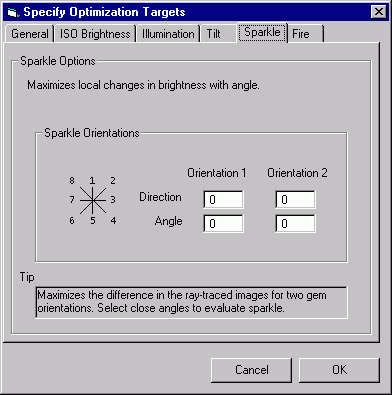
How does one compare ISO brightness with Fire? Or, more specifically, how can we assign numbers to ISO brightness and Fire that can be reasonably added together? The sections below describe how values are assigned to the various targets. To get the most out of BOG, you should review this material.

The Evaluate MF button lets you see a breakdown of the overall Merit Function, given the current mix of targets and weights. It is much more efficient to find a good balance here, rather than through multiple optimization trials. Note, however, that clicking Evaluate MF establishes the targets and weights. Pressing Cancel thereafter will not restore the previous values. Use Load Targets / Save Targets to preserve a good set of optimization values.

Click Ok to accept the current values or Cancel at any time to return to BOG's main window.

 

ISO Brightness

Selecting the ISO Brightness target will maximize the ISO brightness.

ISO brighntess is a measure of the fraction of light returned to the viewer when the stone is viewed under uniform lighting conditions. This optimization target has no options. The GemRay manual provides a complete description of the various lighting models.

The easiest way to understand the lighting models is to imagine the gem, sitting on a flat, infinite plane, usually with its table facet straight up (but see Tilt Performance below). The viewer is directly above the gem, looking down. Light comes from the "sky," bounces around inside the gem, and a certain fraction is directed straight up to the viewer. No light comes from below the plane; from the gem's point of view, everything below the "horizon" is black.

GemRayX offers the "head shadow" option, in which light from within a user-specified angle of zenith cannot enter the stone. You can set this angle within the BOG Preferences panel.

ISO brightness assumes that the "sky" above the gem is uniformly bright, like a heavily clouded day. While this is unrealistic, the ISO value is generally accepted as the best overall measure of a gemstone's brightness. You will often see the ISO brightness quoted in published GemCAD designs.

By the way...
GemRay, like most three dimensional rendering programs, does not actually trace rays from the sky, through the stone, and then up to the viewer. For efficiency, it takes advantage of the reversible property of light and traces rays back from the viewer's eye and through the stone, thereafter assigning a pixel brightness value depending on where the ray hits the sky. For ISO, this will always be the same value, unless the ray is trapped inside the stone or emerges downward into the blackness below the gem's horizon. Doing things "backwards" eliminates the need to trace the vast majority of rays which do not make it into the viewer's eye.

MF Contribution = ISO * ISO_Weight

This target adds the ISO Brightness (in percent) times the weighting factor to the overall merit function.

 

Illumination

This optimization target has no options. Selecting the Illumination target will maximize the ISO - COS brightness difference.

Why is this good? Recall from above that the ISO model assumes uniform lighting, like a cloudy day. The COS brightness model is bright at the zenith, dropping to low intensity at the horizon. Maximizing (ISO-COS) brightness is equivalent to maximizing the gem's response to the inverse of the COS model - that is, one in which the horizon is bright fading to darkness at the zenith. A gem that performs well under these conditions is one which returns a lot of light to the viewer originating from directions other than straight up - for example through the crown breaks and star facets. Such a gem will not suffer as much from the "head shadow" effect. Robert Strickland discusses this effect in the Gemray documentation.

It is not wise to use an Illumination target without an ISO Brightness target, since BOG may come with a gem with large (ISO - COS) value but low overall brightness.

 

 

 

MF Contribution = ( ISO - COS ) * Illum_Weight

This target adds the difference between the ISO and COS Brightnesses (in percent) times the weighting factor to the overall merit function.

 

 

Tilt Performance

This optimization target has several options allowing you to select the direction(s) and angles for evaluating tilt performance. Selecting the Tilt target will minimize the ISO brightness variation as the stone is tilted.

The face-up ISO brightness of a gemstone is only one aspect of its overall performance, and arguably not a terribly important one. Illumination effects (see above) can be significant, and tilt performance will have a profound effect on the subjective appearance of the stone under real-world conditions - a gem is almost never viewed directly from above the table.

Fortunately, Gemray and BOG allow you to raytrace a tilted gem. To use the Tilt optimization target, select one or more Tilt Direction(s) using the check boxes on the left. The symmetry of the stone will help determine which directions are useful - for a round, one direction should suffice, but you may want to check two orientations for a pear. Selecting many Tilt Directions will slow the optimization process considerably,

Set a Maximum Tilt Angle in the appropriate box. BOG will evaluate the ISO brightness for three orientations per Tilt Direction: face up, tilted halfway to the maximum angle, and tilted all the way to the maximum angle (for the values shown here, this would be 0, 10, and 20 degrees in the 12-o'clock direction). It will then calculate the variation in ISO brightness as the stone is tilted (more details here).

Small variation is better. The tilt performance optimization target is therefore different than those associated with brightness, in that it seeks to minimize a quantity, not maximize it. To assign a value for comparison, BOG assumes that zero brightness variation will produce maximum merit, and that variation above a specified quantity gives zero merit. Specify a Brighntess Variation for Zero Merit (BVZM) in the box provided.

BOG 1.2 offers the USFG Tilt Performance target as well as the original BOG version. The USFG criterion is merely the sum of the ISO brightness over a range of angles. See the PlayPen Tutorial for further details.

The tilt performance optimization target is very useful, but less straightforward than that for ISO and Illumination. A more complete description of the Tilt Performance target appears here.

MF Contribution = (1 - Variation / BVZM) * Tilt_Weight

This target contributes the full Tilt_Weight factor to the merit function for zero brightness variation with tilt. If the variation exceeds the Brightness Variation for Zero Merit (BVZM), then zero value is assigned.

 

 

 

 

 

 

Sparkle

Selecting the Sparkle target will maximize the sparkle or "action" of the gemstone.

Sparkle calculates the absolute difference (i.e. always positive numbers) between the raytraces at the two specified angles . Maximizing sparkle means that the gem appearance changes significantly for small angular tilts - in other words it sparkles. Keep the angles close to one another...

 

MF Contribution = Abs(Image_1 - Image_2) * Sparkle_Weight

This target adds the absolute difference between two images raytraced at different angles, times the weighting factor, to the overall merit function.

 

 

Fire or Dispersion

Selecting the Fire target will maximize the fire or dispersion of the gemstone.

Fire calculates the absolute difference (i.e. always positive numbers) between the raytraces for red and blue light. Maximizing fire means that the gem appearance changes significantly for different colours- in other words it has strong dispersion or fire.

BOG 1.2 also offers the GemRayX dispersion brightness optimization target as well as the original BOG version. This brightness value essentially measures the fraction of the gem for which the rays entered the stone at steep angles, leading to greater fire.

 

MF Contribution = Abs(Image_1 - Image_2) * Fire_Weight

This target adds the absolute difference between two images raytraced at different wavelengths, times the weighting factor, to the overall merit function.

 

Back to Main Page.

Documentation maintained by Tom Herbst. Last modified 16-Aug-2005